2.25. Custom PDE class: SIR model

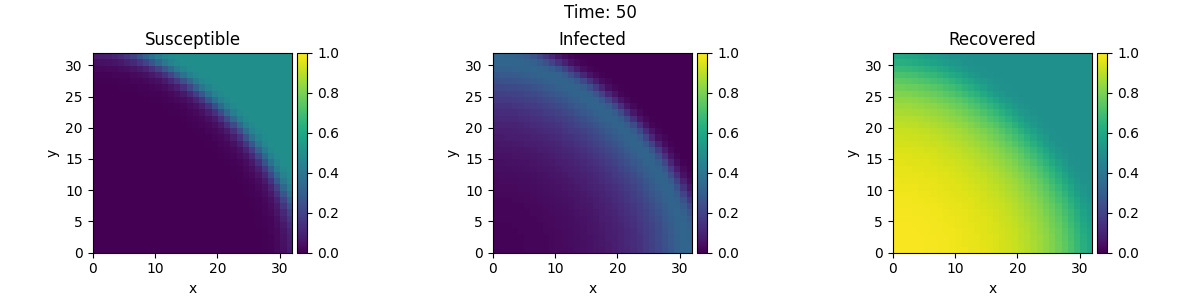
This example implements a spatially coupled SIR model with the following dynamics for the density of susceptible, infected, and recovered individuals:

\[\begin{split}\partial_t s &= D \nabla^2 s - \beta is \\ \partial_t i &= D \nabla^2 i + \beta is - \gamma i \\ \partial_t r &= D \nabla^2 r + \gamma i\end{split}\]

Here, \(D\) is the diffusivity, \(\beta\) the infection rate, and \(\gamma\) the recovery rate.

  0%|          | 0/50.0 [00:00<?, ?it/s]
Initializing:   0%|          | 0/50.0 [00:00<?, ?it/s]
  0%|          | 0/50.0 [00:00<?, ?it/s]
  0%|          | 0.02/50.0 [00:01<43:30, 52.24s/it]
  0%|          | 0.04/50.0 [00:01<21:50, 26.22s/it]
  1%|          | 0.33/50.0 [00:01<02:45,  3.34s/it]
  3%|3         | 1.61/50.0 [00:01<00:40,  1.20it/s]
  8%|8         | 4.23/50.0 [00:01<00:19,  2.32it/s]
 16%|#5        | 7.98/50.0 [00:02<00:13,  3.18it/s]
 25%|##5       | 12.52/50.0 [00:03<00:10,  3.43it/s]
 34%|###3      | 16.78/50.0 [00:04<00:08,  3.79it/s]
 43%|####3     | 21.59/50.0 [00:05<00:07,  3.84it/s]
 52%|#####2    | 26.01/50.0 [00:06<00:05,  4.04it/s]
 62%|######1   | 30.9/50.0 [00:07<00:04,  4.05it/s]
 71%|#######   | 35.36/50.0 [00:08<00:03,  4.18it/s]
 81%|########  | 40.28/50.0 [00:09<00:02,  4.17it/s]
 90%|########9 | 44.76/50.0 [00:10<00:01,  4.27it/s]
 99%|#########9| 49.7/50.0 [00:11<00:00,  4.36it/s]
 99%|#########9| 49.7/50.0 [00:11<00:00,  4.23it/s]
100%|##########| 50.0/50.0 [00:11<00:00,  4.25it/s]
100%|##########| 50.0/50.0 [00:11<00:00,  4.25it/s]

from pde import FieldCollection, PDEBase, PlotTracker, ScalarField, UnitGrid


class SIRPDE(PDEBase):
    """SIR-model with diffusive mobility"""

    def __init__(
        self, beta=0.3, gamma=0.9, diffusivity=0.1, bc="auto_periodic_neumann"
    ):
        super().__init__()
        self.beta = beta  # transmission rate
        self.gamma = gamma  # recovery rate
        self.diffusivity = diffusivity  # spatial mobility
        self.bc = bc  # boundary condition

    def get_state(self, s, i):
        """generate a suitable initial state"""
        norm = (s + i).data.max()  # maximal density
        if norm > 1:
            s /= norm
            i /= norm
        s.label = "Susceptible"
        i.label = "Infected"

        # create recovered field
        r = ScalarField(s.grid, data=1 - s - i, label="Recovered")
        return FieldCollection([s, i, r])

    def evolution_rate(self, state, t=0):
        s, i, r = state
        diff = self.diffusivity
        ds_dt = diff * s.laplace(self.bc) - self.beta * i * s
        di_dt = diff * i.laplace(self.bc) + self.beta * i * s - self.gamma * i
        dr_dt = diff * r.laplace(self.bc) + self.gamma * i
        return FieldCollection([ds_dt, di_dt, dr_dt])


eq = SIRPDE(beta=2, gamma=0.1)

# initialize state
grid = UnitGrid([32, 32])
s = ScalarField(grid, 1)
i = ScalarField(grid, 0)
i.data[0, 0] = 1
state = eq.get_state(s, i)

# simulate the pde
tracker = PlotTracker(interval=10, plot_args={"vmin": 0, "vmax": 1})
sol = eq.solve(state, t_range=50, dt=1e-2, tracker=["progress", tracker])