2.20 Custom Class for coupled PDEs

This example shows how to solve a set of coupled PDEs, the spatially coupled FitzHugh–Nagumo model, which is a simple model for the excitable dynamics of coupled Neurons:

\[\begin{split}\partial_t u &= \nabla^2 u + u (u - \alpha) (1 - u) + w \\ \partial_t w &= \epsilon u\end{split}\]

Here, \(\alpha\) denotes the external stimulus and \(\epsilon\) defines the recovery time scale. We implement this as a custom PDE class below.

  0%|          | 0/100.0 [00:00<?, ?it/s]
Initializing:   0%|          | 0/100.0 [00:00<?, ?it/s]
  0%|          | 0/100.0 [00:00<?, ?it/s]
  0%|          | 0.27/100.0 [00:00<01:10,  1.41it/s]
  1%|          | 0.87/100.0 [00:00<00:26,  3.79it/s]
  4%|▍         | 3.94/100.0 [00:00<00:10,  9.41it/s]
 11%|█         | 11.01/100.0 [00:00<00:07, 12.45it/s]
 21%|██▏       | 21.37/100.0 [00:01<00:06, 12.86it/s]
 33%|███▎      | 33.13/100.0 [00:02<00:04, 13.66it/s]
 47%|████▋     | 46.58/100.0 [00:03<00:03, 13.81it/s]
 60%|██████    | 60.4/100.0 [00:04<00:02, 14.01it/s]
 75%|███████▍  | 74.65/100.0 [00:05<00:01, 14.09it/s]
 89%|████████▉ | 89.0/100.0 [00:06<00:00, 14.18it/s]
 89%|████████▉ | 89.0/100.0 [00:07<00:00, 12.68it/s]
100%|██████████| 100.0/100.0 [00:07<00:00, 14.24it/s]
100%|██████████| 100.0/100.0 [00:07<00:00, 14.24it/s]

from pde import FieldCollection, PDEBase, UnitGrid


class FitzhughNagumoPDE(PDEBase):
    """FitzHugh–Nagumo model with diffusive coupling"""

    def __init__(self, stimulus=0.5, τ=10, a=0, b=0, bc="auto_periodic_neumann"):
        super().__init__()
        self.bc = bc
        self.stimulus = stimulus
        self.τ = τ
        self.a = a
        self.b = b

    def evolution_rate(self, state, t=0):
        v, w = state  # membrane potential and recovery variable

        v_t = v.laplace(bc=self.bc) + v - v**3 / 3 - w + self.stimulus
        w_t = (v + self.a - self.b * w) / self.τ

        return FieldCollection([v_t, w_t])


grid = UnitGrid([32, 32])
state = FieldCollection.scalar_random_uniform(2, grid)

eq = FitzhughNagumoPDE()
result = eq.solve(state, t_range=100, dt=0.01)
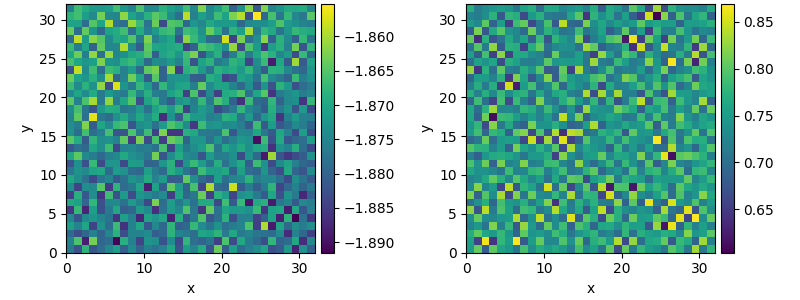
result.plot()