2.8. Diffusion on a Cartesian grid

This example shows how to solve the diffusion equation on a Cartesian grid.

  0%|          | 0/1.0 [00:00<?, ?it/s]
Initializing:   0%|          | 0/1.0 [00:00<?, ?it/s]/home/docs/checkouts/readthedocs.org/user_builds/py-pde/checkouts/0.30.0/pde/grids/boundaries/local.py:1822: NumbaDeprecationWarning: The 'nopython' keyword argument was not supplied to the 'numba.jit' decorator. The implicit default value for this argument is currently False, but it will be changed to True in Numba 0.59.0. See https://numba.readthedocs.io/en/stable/reference/deprecation.html#deprecation-of-object-mode-fall-back-behaviour-when-using-jit for details.
  def virtual_point(

  0%|          | 0/1.0 [00:05<?, ?it/s]
  1%|1         | 0.01/1.0 [00:05<08:39, 524.88s/it]
  3%|3         | 0.03/1.0 [00:05<02:49, 174.97s/it]
  3%|3         | 0.03/1.0 [00:05<02:49, 175.02s/it]
100%|##########| 1.0/1.0 [00:05<00:00,  5.25s/it]
100%|##########| 1.0/1.0 [00:05<00:00,  5.25s/it]

from pde import CartesianGrid, DiffusionPDE, ScalarField

grid = CartesianGrid([[-1, 1], [0, 2]], [30, 16])  # generate grid
state = ScalarField(grid)  # generate initial condition
state.insert([0, 1], 1)

eq = DiffusionPDE(0.1)  # define the pde
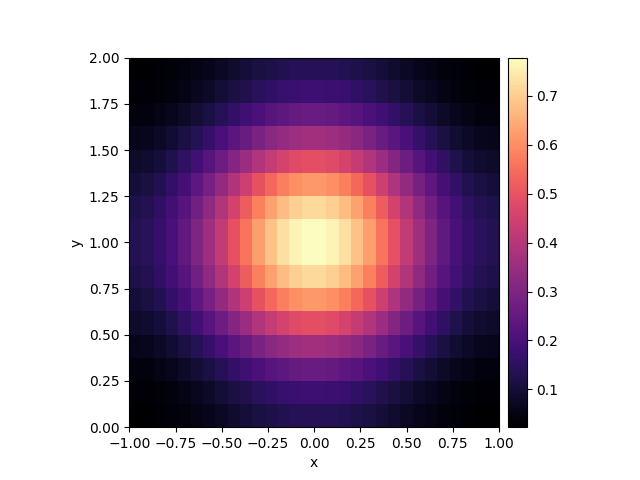
result = eq.solve(state, t_range=1, dt=0.01)
result.plot(cmap="magma")