Note
Go to the end to download the full example code
2.14. Brusselator - Using the PDE class
This example uses the PDE class to implement the
Brusselator with spatial
coupling,
\[\begin{split}\partial_t u &= D_0 \nabla^2 u + a - (1 + b) u + v u^2 \\
\partial_t v &= D_1 \nabla^2 v + b u - v u^2\end{split}\]
Here, \(D_0\) and \(D_1\) are the respective diffusivity and the parameters \(a\) and \(b\) are related to reaction rates.
Note that the same result can also be achieved with a full implementation of a custom class, which allows for more flexibility at the cost of code complexity.
from pde import PDE, FieldCollection, PlotTracker, ScalarField, UnitGrid
# define the PDE
a, b = 1, 3
d0, d1 = 1, 0.1
eq = PDE(
{
"u": f"{d0} * laplace(u) + {a} - ({b} + 1) * u + u**2 * v",
"v": f"{d1} * laplace(v) + {b} * u - u**2 * v",
}
)
# initialize state
grid = UnitGrid([64, 64])
u = ScalarField(grid, a, label="Field $u$")
v = b / a + 0.1 * ScalarField.random_normal(grid, label="Field $v$")
state = FieldCollection([u, v])
# simulate the pde
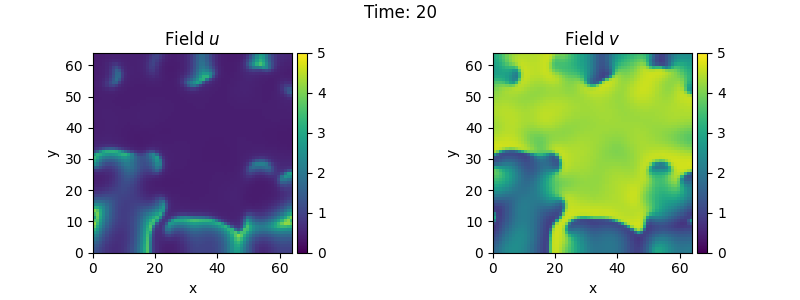
tracker = PlotTracker(interval=1, plot_args={"vmin": 0, "vmax": 5})
sol = eq.solve(state, t_range=20, dt=1e-3, tracker=tracker)
Total running time of the script: ( 0 minutes 30.915 seconds)