Note
Click here to download the full example code
2.15. Diffusion equation with spatial dependence¶
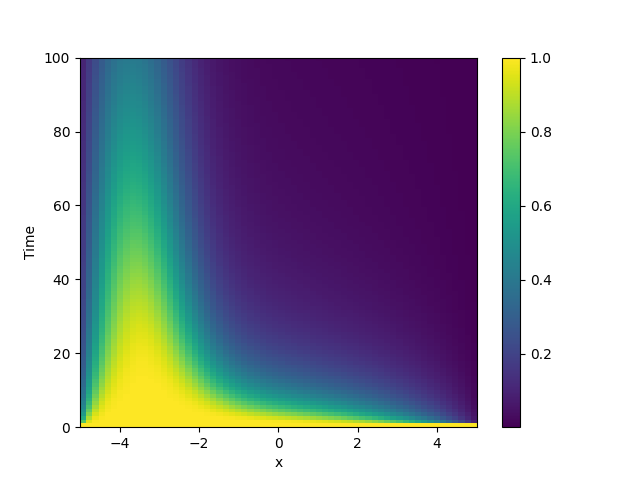
This example solve the Diffusion equation with a heterogeneous diffusivity:
\[\partial_t c = \nabla\bigr( D(\boldsymbol r) \nabla c \bigr)\]
using the PDE class. In particular, we consider
\(D(x) = 1.01 + \tanh(x)\), which gives a low diffusivity on the left side of the
domain.
Note that the naive implementation,
PDE({"c": "divergence((1.01 + tanh(x)) * gradient(c))"}), has numerical
instabilities. This is because two finite difference approximations are nested. To
arrive at a more stable numerical scheme, it is advisable to expand the divergence,
\[\partial_t c = D \nabla^2 c + \nabla D . \nabla c\]
from pde import PDE, CartesianGrid, MemoryStorage, ScalarField, plot_kymograph
# Expanded definition of the PDE
diffusivity = "1.01 + tanh(x)"
term_1 = f"({diffusivity}) * laplace(c)"
term_2 = f"dot(gradient({diffusivity}), gradient(c))"
eq = PDE({"c": f"{term_1} + {term_2}"}, bc={"value": 0})
grid = CartesianGrid([[-5, 5]], 64) # generate grid
field = ScalarField(grid, 1) # generate initial condition
storage = MemoryStorage() # store intermediate information of the simulation
res = eq.solve(field, 100, dt=1e-3, tracker=storage.tracker(1)) # solve the PDE
plot_kymograph(storage) # visualize the result in a space-time plot
Total running time of the script: ( 0 minutes 11.415 seconds)