Note
Click here to download the full example code
2.8. Diffusion on a Cartesian grid¶
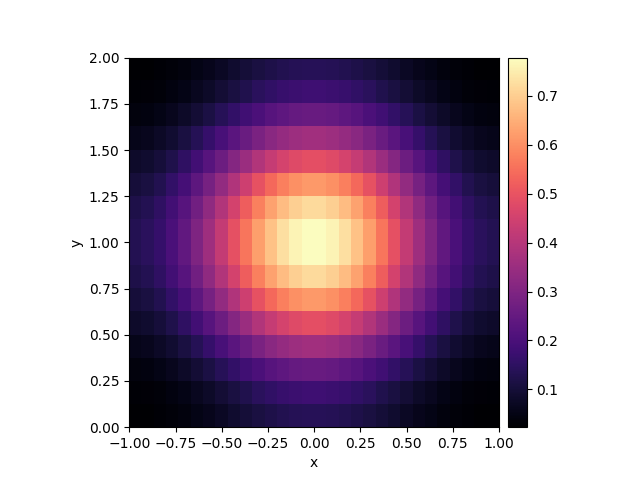
This example shows how to solve the diffusion equation on a Cartesian grid.
Out:
0%| | 0/1.0 [00:00<?, ?it/s]
Initializing: 0%| | 0/1.0 [00:00<?, ?it/s]
0%| | 0/1.0 [00:06<?, ?it/s]
1%|1 | 0.01/1.0 [00:07<12:39, 767.34s/it]
2%|2 | 0.02/1.0 [00:08<07:09, 438.71s/it]
3%|3 | 0.03/1.0 [00:08<04:43, 292.48s/it]
27%|##7 | 0.27/1.0 [00:08<00:23, 32.50s/it]
27%|##7 | 0.27/1.0 [00:08<00:23, 32.50s/it]
100%|##########| 1.0/1.0 [00:08<00:00, 8.78s/it]
100%|##########| 1.0/1.0 [00:08<00:00, 8.78s/it]
from pde import CartesianGrid, DiffusionPDE, ScalarField
grid = CartesianGrid([[-1, 1], [0, 2]], [30, 16]) # generate grid
state = ScalarField(grid) # generate initial condition
state.insert([0, 1], 1)
eq = DiffusionPDE(0.1) # define the pde
result = eq.solve(state, t_range=1, dt=0.01)
result.plot(cmap="magma")
Total running time of the script: ( 0 minutes 8.948 seconds)