4.2.1. pde.grids.boundaries package
This package contains classes for handling the boundary conditions of fields.
4.2.1.1. Boundary conditions
The mathematical details of boundary conditions for partial differential equations are
treated in more detail in the
documentation document.
Since the pde package only supports orthogonal grids, boundary conditions need to
be applied at the end of each axis.
Consequently, methods expecting boundary conditions typically receive a list of
conditions for each axes:
field = ScalarField(UnitGrid([16, 16], periodic=[True, False]))
field.laplace(bc=[bc_x, bc_y])
If an axis is periodic (like the first one in the example above), the only valid boundary conditions are ‘periodic’ and its cousin ‘anti-periodic’, which imposes opposite signs on both sides. For non-periodic axes (e.g., the second axis), different boundary conditions can be specified for the lower and upper end of the axis, which is done using a tuple of two conditions. Typical choices for individual conditions are Dirichlet conditions that enforce a value NUM (specified by {‘value’: NUM}) and Neumann conditions that enforce the value DERIV for the derivative in the normal direction (specified by {‘derivative’: DERIV}). The specific choices for the example above could be
bc_x = "periodic"
bc_y = ({"value": 2}, {"derivative": -1})
which enforces a value of 2 at the lower side of the y-axis and a derivative (in outward normal direction) of -1 on the upper side. Instead of plain numbers, which enforce the same condition along the whole boundary, expressions can be used to support inhomogeneous boundary conditions. These mathematical expressions are given as a string that can be parsed by sympy. They can depend on all coordinates of the grid. An alternative boundary condition to the example above could thus read
bc_y = ({"value": "y**2"}, {"derivative": "-sin(x)"})
Warning
To interpret arbitrary expressions, the package uses exec(). It
should therefore not be used in a context where malicious input could occur.
Inhomogeneous values can also be specified by directly supplying an array, whose shape needs to be compatible with the boundary, i.e., it needs to have the same shape as the grid but with the dimension of the axis along which the boundary is specified removed.
The package also supports mixed boundary conditions (depending on both the value and the derivative of the field) and imposing a second derivative. An example is
bc_y = ({"type": "mixed", "value": 2, "const": 7},
{"curvature": 2})
which enforces the condition \(\partial_n c + 2 c = 7\) and \(\partial^2_n c = 2\) onto the field \(c\) on the lower and upper side of the axis, respectively.
Beside the full specification of the boundary conditions, various short-hand
notations are supported. If both sides of an axis have the same boundary
condition, only one needs to be specified (instead of the tuple). For instance,
bc_y = {'value': 2} imposes a value of 2 on both sides of the y-axis.
Similarly, if all axes have the same boundary conditions, only one axis needs to
be specified (instead of the list). For instance, the following example
field = ScalarField(UnitGrid([16, 16], periodic=False))
field.laplace(bc={"value": 2})
imposes a value of 2 on all sides of the grid. Finally, the special values ‘auto_periodic_neumann’ and ‘auto_periodic_dirichlet’ impose periodic boundary conditions for periodic axis and a vanishing derivative or value otherwise. For example,
field = ScalarField(UnitGrid([16, 16], periodic=[True, False]))
field.laplace(bc="auto_periodic_neumann")
enforces periodic boundary conditions on the first axis, while the second one has standard Neumann conditions.
Note
Derivatives are given relative to the outward normal vector, such that positive derivatives correspond to a function that increases across the boundary.
4.2.1.2. Boundaries overview
The boundaries package defines the following classes:
Local boundary conditions:
DirichletBC: Imposing a constant value of the field at the boundaryExpressionValueBC: Imposing the value of the field at the boundary given by an expression or a python functionNeumannBC: Imposing a constant derivative of the field in the outward normal direction at the boundaryExpressionDerivativeBC: Imposing the derivative of the field in the outward normal direction at the boundary given by an expression or a python functionMixedBC: Imposing the derivative of the field in the outward normal direction proportional to its value at the boundaryCurvatureBC: Imposing a constant second derivative (curvature) of the field at the boundary
There are corresponding classes that only affect the normal component of a field, which
can be useful when dealing with vector and tensor fields:
NormalDirichletBC,
NormalNeumannBC,
NormalMixedBC, and
NormalCurvatureBC.
Boundaries for an axis:
BoundaryPair: Uses the local boundary conditions to specify the two boundaries along an axisBoundaryPeriodic: Indicates that an axis has periodic boundary conditions
Boundaries for all axes of a grid:
Boundaries: Collection of boundaries to describe conditions for all axes
Inheritance structure of the classes:
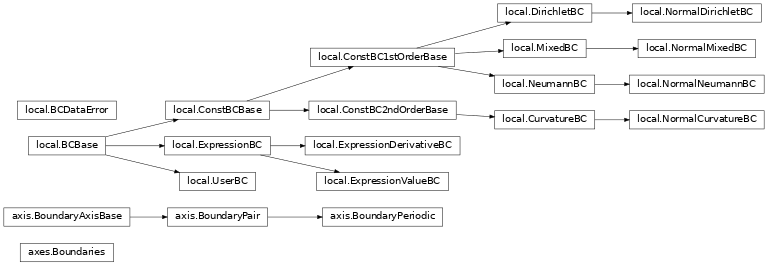
The details of the classes are explained below: