Note
Go to the end to download the full example code
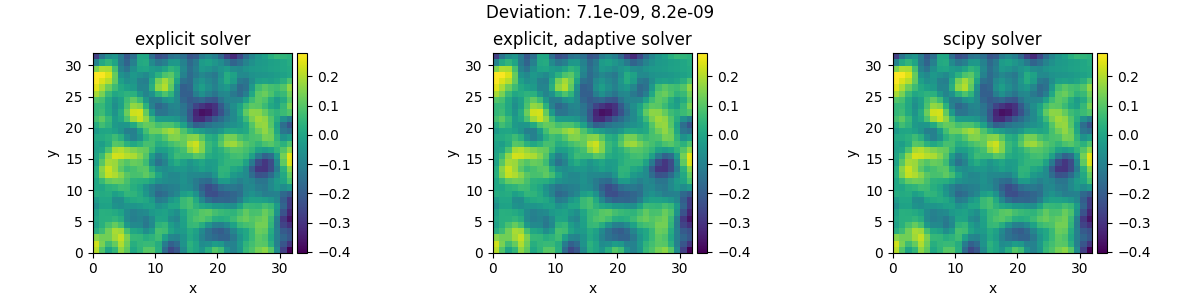
2.24 Solver comparison
This example shows how to set up solvers explicitly and how to extract diagnostic information.
Diagnostic information from first run:
{'controller': {'t_start': 0, 't_end': 1.0, 'profiler': {'solver': 0.057310991999997896, 'tracker': 4.4093000013845085e-05, 'compilation': 4.5087980099999925}, 'jit_count': {'make_stepper': 11, 'simulation': 0}, 'solver_start': '2024-04-18 18:31:35.800805', 'successful': True, 'stop_reason': 'Reached final time', 'solver_duration': '0:00:00.057353', 't_final': 1.0, 'process_count': 1}, 'package_version': 'unknown', 'solver': {'class': 'ExplicitSolver', 'pde_class': 'DiffusionPDE', 'dt': 0.001, 'steps': 1000, 'state_modifications': 0.0, 'stochastic': False, 'scheme': 'euler', 'backend': 'numba'}}
Diagnostic information from second run:
{'controller': {'t_start': 0, 't_end': 1.0, 'profiler': {'solver': 0.20531472599998324, 'tracker': 5.655600000409322e-05, 'compilation': 1.183743576000012}, 'jit_count': {'make_stepper': 2, 'simulation': 0}, 'solver_start': '2024-04-18 18:31:37.042804', 'successful': True, 'stop_reason': 'Reached final time', 'solver_duration': '0:00:00.205367', 't_final': 1.0, 'process_count': 1}, 'package_version': 'unknown', 'solver': {'class': 'ExplicitSolver', 'pde_class': 'DiffusionPDE', 'dt': 0.001, 'dt_adaptive': True, 'steps': 12, 'stochastic': False, 'state_modifications': 0.0, 'dt_statistics': {'min': 0.001, 'max': 0.16557795391427504, 'mean': 0.08333333333333333, 'std': 0.05133174820289221, 'count': 12.0}, 'scheme': 'runge-kutta', 'backend': 'numba'}}
Diagnostic information from third run:
{'controller': {'t_start': 0, 't_end': 1.0, 'profiler': {'solver': 0.003476933999991161, 'tracker': 4.6714000006886636e-05, 'compilation': 0.6326560560000019}, 'jit_count': {'make_stepper': 1, 'simulation': 0}, 'solver_start': '2024-04-18 18:31:39.307811', 'successful': True, 'stop_reason': 'Reached final time', 'solver_duration': '0:00:00.003520', 't_final': 1.0, 'process_count': 1}, 'package_version': 'unknown', 'solver': {'class': 'ScipySolver', 'pde_class': 'DiffusionPDE', 'dt': None, 'steps': 50, 'stochastic': False, 'backend': 'numba'}}
import pde
# initialize the grid, an initial condition, and the PDE
grid = pde.UnitGrid([32, 32])
field = pde.ScalarField.random_uniform(grid, -1, 1)
eq = pde.DiffusionPDE()
# try the explicit solver
solver1 = pde.ExplicitSolver(eq)
controller1 = pde.Controller(solver1, t_range=1, tracker=None)
sol1 = controller1.run(field, dt=1e-3)
sol1.label = "explicit solver"
print("Diagnostic information from first run:")
print(controller1.diagnostics)
print()
# try an explicit solver with adaptive time steps
solver2 = pde.ExplicitSolver(eq, scheme="runge-kutta", adaptive=True)
controller2 = pde.Controller(solver2, t_range=1, tracker=None)
sol2 = controller2.run(field, dt=1e-3)
sol2.label = "explicit, adaptive solver"
print("Diagnostic information from second run:")
print(controller2.diagnostics)
print()
# try the standard scipy solver
solver3 = pde.ScipySolver(eq)
controller3 = pde.Controller(solver3, t_range=1, tracker=None)
sol3 = controller3.run(field)
sol3.label = "scipy solver"
print("Diagnostic information from third run:")
print(controller3.diagnostics)
print()
# plot both fields and give the deviation as the title
title = f"Deviation: {((sol1 - sol2)**2).average:.2g}, {((sol1 - sol3)**2).average:.2g}"
pde.FieldCollection([sol1, sol2, sol3]).plot(title=title)
Total running time of the script: (0 minutes 8.526 seconds)