Note
Go to the end to download the full example code
2.12 1D problem - Using PDE class
This example implements a PDE that is only defined in one dimension. Here, we chose the Korteweg-de Vries equation, given by
\[\partial_t \phi = 6 \phi \partial_x \phi - \partial_x^3 \phi\]
which we implement using the PDE.
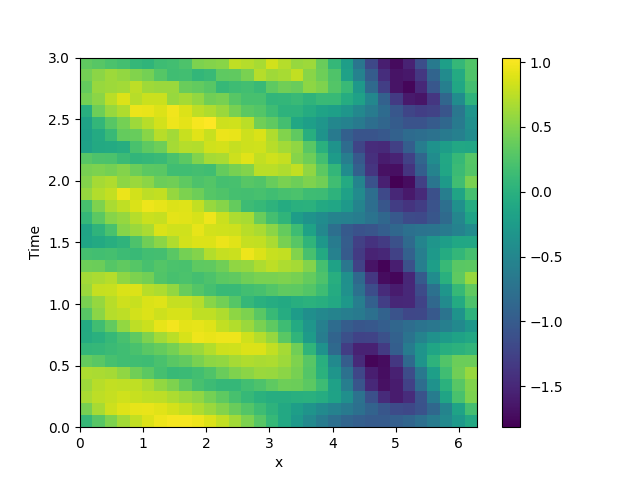
from math import pi
from pde import PDE, CartesianGrid, MemoryStorage, ScalarField, plot_kymograph
# initialize the equation and the space
eq = PDE({"φ": "6 * φ * d_dx(φ) - laplace(d_dx(φ))"})
grid = CartesianGrid([[0, 2 * pi]], [32], periodic=True)
state = ScalarField.from_expression(grid, "sin(x)")
# solve the equation and store the trajectory
storage = MemoryStorage()
eq.solve(state, t_range=3, solver="scipy", tracker=storage.tracker(0.1))
# plot the trajectory as a space-time plot
plot_kymograph(storage)
Total running time of the script: (0 minutes 8.552 seconds)