2.13 Heterogeneous boundary conditions

This example implements a spatially coupled SIR model with the following dynamics for the density of susceptible, infected, and recovered individuals:

\[\begin{split}\partial_t s &= D \nabla^2 s - \beta is \\ \partial_t i &= D \nabla^2 i + \beta is - \gamma i \\ \partial_t r &= D \nabla^2 r + \gamma i\end{split}\]

Here, \(D\) is the diffusivity, \(\beta\) the infection rate, and \(\gamma\) the recovery rate.

  0%|          | 0/10.0 [00:00<?, ?it/s]
Initializing:   0%|          | 0/10.0 [00:00<?, ?it/s]
  0%|          | 0/10.0 [00:00<?, ?it/s]
  3%|▎         | 0.26/10.0 [00:00<00:07,  1.26it/s]
  8%|▊         | 0.81/10.0 [00:00<00:02,  3.33it/s]
 37%|███▋      | 3.71/10.0 [00:00<00:00,  8.47it/s]
 37%|███▋      | 3.71/10.0 [00:00<00:01,  4.35it/s]
100%|██████████| 10.0/10.0 [00:00<00:00, 11.72it/s]
100%|██████████| 10.0/10.0 [00:00<00:00, 11.72it/s]

import numpy as np

from pde import CartesianGrid, DiffusionPDE, ScalarField

# define grid and an initial state
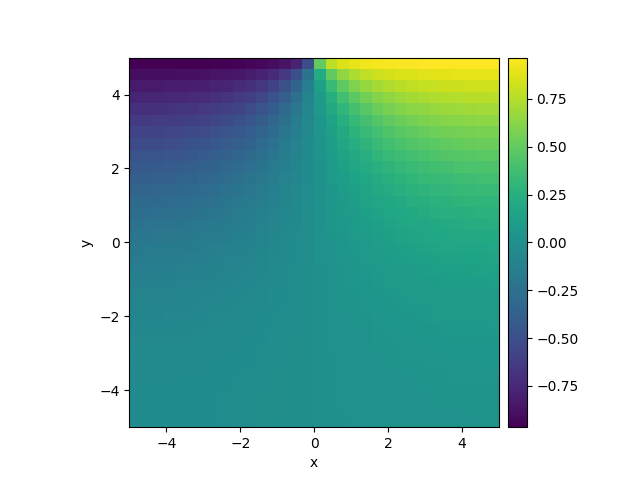
grid = CartesianGrid([[-5, 5], [-5, 5]], 32)
field = ScalarField(grid)


# define the boundary conditions, which here are calculated from a function
def bc_value(adjacent_value, dx, x, y, t):
    """return boundary value"""
    return np.sign(x)


bc_x = "derivative"
bc_y = ["derivative", {"value_expression": bc_value}]

# define and solve a simple diffusion equation
eq = DiffusionPDE(bc=[bc_x, bc_y])
res = eq.solve(field, t_range=10, dt=0.01, backend="numpy")
res.plot()