4.2.1.5. pde.grids.boundaries.local module
This module contains classes for handling a single boundary of a non-periodic axis. Since an axis has two boundary, we simply distinguish them by a boolean flag upper, which is True for the side of the axis with the larger coordinate.
The module currently supports the following standard boundary conditions:
DirichletBC: Imposing the value of a field at the boundaryNeumannBC: Imposing the derivative of a field in the outward normal direction at the boundaryMixedBC: Imposing the derivative of a field in the outward normal direction proportional to its value at the boundaryCurvatureBC: Imposing the second derivative (curvature) of a field at the boundary
There are also variants of these boundary conditions that only affect the normal
components of a vector or tensor field:
NormalDirichletBC,
NormalNeumannBC,
NormalMixedBC, and
NormalCurvatureBC.
Finally, there are more specialized classes, which offer greater flexibility, but might also require a slightly deeper understanding for proper use:
ExpressionValueBC: Imposing the value of a field at the boundary based on a mathematical expression or a python function.ExpressionDerivativeBC: Imposing the derivative of a field in the outward normal direction at the boundary based on a mathematical expression or a python function.UserBC: Allows full control for setting virtual points, values, or derivatives. The boundary conditions are never enforced automatically. It is thus the user’s responsibility to ensure virtual points are set correctly before operators are applied. To set boundary conditions a dictionary{TARGET: value}must be supplied as argument args toset_ghost_cells()or the numba equivalent. Here, TARGET determines how the value is interpreted and what boundary condition is actually enforced: the value of the virtual points directly (virtual_point), the value of the field at the boundary (value) or the outward derivative of the field at the boundary (derivative).
Note that derivatives are generally given in the direction of the outward normal vector, such that positive derivatives correspond to a function that increases across the boundary.
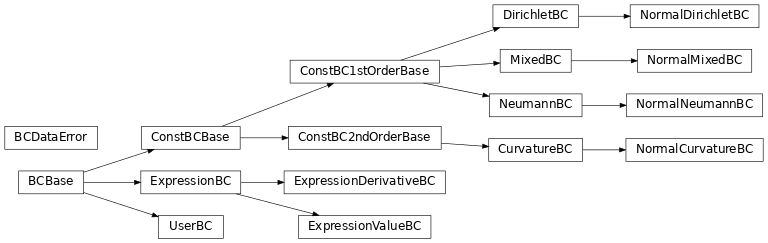
Inheritance structure of the classes:
- class BCBase(grid, axis, upper, *, rank=0)[source]
Bases:
objectrepresents a single boundary in an BoundaryPair instance
- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
- check_value_rank(rank)[source]
check whether the values at the boundaries have the correct rank
- Parameters:
rank (int) – The tensorial rank of the field for this boundary condition
- Return type:
None
- Throws:
RuntimeError: if the value does not have rank rank
- classmethod from_data(grid, axis, upper, data, *, rank=0)[source]
create boundary from some data
- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Indicates whether this boundary condition is associated with the upper or lower side of the axis.
rank (int) – The tensorial rank of the field for this boundary condition
- Returns:
the instance created from the data
- Return type:
- Throws:
ValueError if data cannot be interpreted as a boundary condition
- classmethod from_dict(grid, axis, upper, data, *, rank=0)[source]
create boundary from data given in dictionary
- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Indicates whether this boundary condition is associated with the upper or lower side of the axis.
data (dict) – The dictionary defining the boundary condition
rank (int) – The tensorial rank of the field for this boundary condition
- Return type:
- classmethod from_str(grid, axis, upper, condition, *, rank=0, **kwargs)[source]
creates boundary from a given string identifier
- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Indicates whether this boundary condition is associated with the upper or lower side of the axis.
condition (str) – Identifies the boundary condition
rank (int) – The tensorial rank of the field for this boundary condition
**kwargs – Additional arguments passed to the constructor
- Return type:
- classmethod get_help()[source]
Return information on how boundary conditions can be set
- Return type:
- get_mathematical_representation(field_name='C')[source]
return mathematical representation of the boundary condition
- make_ghost_cell_sender()[source]
return function that might mpi_send data to set ghost cells for this boundary
- Return type:
- make_ghost_cell_setter()[source]
return function that sets the ghost cells for this boundary
- Return type:
- normal: bool = False
determines whether the boundary condition only affects normal components.
If this flag is False, boundary conditions must specify values for all components of the field. If True, only the normal components at the boundary are specified.
- Type:
- exception BCDataError[source]
Bases:
ValueErrorexception that signals that incompatible data was supplied for the BC
- class ConstBC1stOrderBase(grid, axis, upper, *, rank=0, value=0)[source]
Bases:
ConstBCBaserepresents a single boundary in an BoundaryPair instance
Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur. However, the function is safe when value cannot be an arbitrary string.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
normal (bool) – Flag indicating whether the condition is only applied in the normal direction.
value (float or str or
ndarray) – a value stored with the boundary condition. The interpretation of this value depends on the type of boundary condition. If value is a single value (or tensor in case of tensorial boundary conditions), the same value is applied to all points. Inhomogeneous boundary conditions are possible by supplying an expression as a string, which then may depend on the axes names of the respective grid.
- get_virtual_point(arr, idx=None)[source]
calculate the value of the virtual point outside the boundary
- Parameters:
arr (array) – The data values associated with the grid
idx (tuple) – The index of the point to evaluate. This is a tuple of length grid.num_axes with the either -1 or dim as the entry for the axis associated with this boundary condition. Here, dim is the dimension of the axis. The index is optional if dim == 1.
- Returns:
Value at the virtual support point
- Return type:
- make_adjacent_evaluator()[source]
returns a function evaluating the value adjacent to a given point
- Returns:
A function with signature (arr_1d, i_point, bc_idx), where arr_1d is the one-dimensional data array (the data points along the axis perpendicular to the boundary), i_point is the index into this array for the current point and bc_idx are the remaining indices of the current point, which indicate the location on the boundary plane. The result of the function is the data value at the adjacent point along the axis associated with this boundary condition in the upper (lower) direction when upper is True (False).
- Return type:
function
- make_virtual_point_evaluator()[source]
returns a function evaluating the value at the virtual support point
- Returns:
A function that takes the data array and an index marking the current point, which is assumed to be a virtual point. The result is the data value at this point, which is calculated using the boundary condition.
- Return type:
function
- class ConstBC2ndOrderBase(grid, axis, upper, *, rank=0, value=0)[source]
Bases:
ConstBCBaseabstract base class for boundary conditions of 2nd order
Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur. However, the function is safe when value cannot be an arbitrary string.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
normal (bool) – Flag indicating whether the condition is only applied in the normal direction.
value (float or str or
ndarray) – a value stored with the boundary condition. The interpretation of this value depends on the type of boundary condition. If value is a single value (or tensor in case of tensorial boundary conditions), the same value is applied to all points. Inhomogeneous boundary conditions are possible by supplying an expression as a string, which then may depend on the axes names of the respective grid.
- get_virtual_point(arr, idx=None)[source]
calculate the value of the virtual point outside the boundary
- Parameters:
arr (array) – The data values associated with the grid
idx (tuple) – The index of the point to evaluate. This is a tuple of length grid.num_axes with the either -1 or dim as the entry for the axis associated with this boundary condition. Here, dim is the dimension of the axis. The index is optional if dim == 1.
- Returns:
Value at the virtual support point
- Return type:
- abstract get_virtual_point_data()[source]
return data suitable for calculating virtual points
- Returns:
the data associated with this virtual point
- Return type:
- make_adjacent_evaluator()[source]
returns a function evaluating the value adjacent to a given point
- Returns:
A function with signature (arr_1d, i_point, bc_idx), where arr_1d is the one-dimensional data array (the data points along the axis perpendicular to the boundary), i_point is the index into this array for the current point and bc_idx are the remaining indices of the current point, which indicate the location on the boundary plane. The result of the function is the data value at the adjacent point along the axis associated with this boundary condition in the upper (lower) direction when upper is True (False).
- Return type:
function
- make_virtual_point_evaluator()[source]
returns a function evaluating the value at the virtual support point
- Returns:
A function that takes the data array and an index marking the current point, which is assumed to be a virtual point. The result is the data value at this point, which is calculated using the boundary condition.
- Return type:
function
- class ConstBCBase(grid, axis, upper, *, rank=0, value=0)[source]
Bases:
BCBasebase class representing a boundary whose virtual point is set from constants
Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur. However, the function is safe when value cannot be an arbitrary string.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
normal (bool) – Flag indicating whether the condition is only applied in the normal direction.
value (float or str or
ndarray) – a value stored with the boundary condition. The interpretation of this value depends on the type of boundary condition. If value is a single value (or tensor in case of tensorial boundary conditions), the same value is applied to all points. Inhomogeneous boundary conditions are possible by supplying an expression as a string, which then may depend on the axes names of the respective grid.
- copy(upper=None, rank=None, value=None)[source]
return a copy of itself, but with a reference to the same grid
- Parameters:
- Return type:
- link_value(value)[source]
link value of this boundary condition to external array
- Parameters:
value (ndarray) –
- to_subgrid(subgrid)[source]
converts this boundary condition to one valid for a given subgrid
- Parameters:
subgrid (
GridBase) – Grid of the new boundary conditionsself (ConstBCBase) –
- Returns:
Boundary conditions valid on the subgrid
- Return type:
- class CurvatureBC(grid, axis, upper, *, rank=0, value=0)[source]
Bases:
ConstBC2ndOrderBaserepresents a boundary condition imposing the 2nd normal derivative at the boundary
Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur. However, the function is safe when value cannot be an arbitrary string.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
normal (bool) – Flag indicating whether the condition is only applied in the normal direction.
value (float or str or
ndarray) – a value stored with the boundary condition. The interpretation of this value depends on the type of boundary condition. If value is a single value (or tensor in case of tensorial boundary conditions), the same value is applied to all points. Inhomogeneous boundary conditions are possible by supplying an expression as a string, which then may depend on the axes names of the respective grid.
- get_mathematical_representation(field_name='C')[source]
return mathematical representation of the boundary condition
- get_virtual_point_data()[source]
return data suitable for calculating virtual points
- Returns:
the data structure associated with this virtual point
- Return type:
- class DirichletBC(grid, axis, upper, *, rank=0, value=0)[source]
Bases:
ConstBC1stOrderBaserepresents a boundary condition imposing the value
Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur. However, the function is safe when value cannot be an arbitrary string.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
normal (bool) – Flag indicating whether the condition is only applied in the normal direction.
value (float or str or
ndarray) – a value stored with the boundary condition. The interpretation of this value depends on the type of boundary condition. If value is a single value (or tensor in case of tensorial boundary conditions), the same value is applied to all points. Inhomogeneous boundary conditions are possible by supplying an expression as a string, which then may depend on the axes names of the respective grid.
- get_mathematical_representation(field_name='C')[source]
return mathematical representation of the boundary condition
- get_virtual_point_data(compiled=False)[source]
return data suitable for calculating virtual points
- Parameters:
compiled (bool) – Flag indicating whether a compiled version is required, which automatically takes updated values into account when it is used in numba-compiled code.
- Returns:
the data structure associated with this virtual point
- Return type:
BC1stOrderData
- class ExpressionBC(grid, axis, upper, *, rank=0, value=0, target='virtual_point')[source]
Bases:
BCBaserepresents a boundary whose virtual point is calculated from an expression
The expression is given as a string and will be parsed by
sympy. The expression can contain typical mathematical operators and may depend on the value at the last support point next to the boundary (value), spatial coordinates defined by the grid marking the boundary point (e.g., x or r), and time t.Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
value (float or str or callable) – An expression that determines the value of the boundary condition. Alternatively, this can be a (jitable, vectorized) function with signature (adjacent_value, dx, *coords, t) that determines the value of target from the closest field value adjacent_value, the spatial discretization dx in the direction perpendicular to the wall, the spatial coordinates of the wall point, and time t.
target (str) – Selects which value is actually set. Possible choices include value, derivative, and virtual_point.
- copy(upper=None, rank=None)[source]
return a copy of itself, but with a reference to the same grid
- Parameters:
self (ExpressionBC) –
upper (bool | None) –
rank (int | None) –
- Return type:
- get_mathematical_representation(field_name='C')[source]
return mathematical representation of the boundary condition
- make_virtual_point_evaluator()[source]
returns a function evaluating the value at the virtual support point
- Returns:
A function that takes the data array and an index marking the current point, which is assumed to be a virtual point. The result is the data value at this point, which is calculated using the boundary condition.
- Return type:
function
- set_ghost_cells(data_full, *, args=None)[source]
set the ghost cell values for this boundary
- Parameters:
data_full (
ndarray) – The full field data including ghost pointsargs – Additional arguments that might be supported by special boundary conditions.
- Return type:
None
- to_subgrid(subgrid)[source]
converts this boundary condition to one valid for a given subgrid
- Parameters:
subgrid (
GridBase) – Grid of the new boundary conditionsself (ExpressionBC) –
- Returns:
Boundary conditions valid on the subgrid
- Return type:
- class ExpressionDerivativeBC(grid, axis, upper, *, rank=0, value=0, target='derivative')[source]
Bases:
ExpressionBCrepresents a boundary whose outward derivative is calculated from an expression
The expression is given as a string and will be parsed by
sympy. The expression can contain typical mathematical operators and may depend on the value at the last support point next to the boundary (value), spatial coordinates defined by the grid marking the boundary point (e.g., x or r), and time t.Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
value (float or str or callable) – An expression that determines the value of the boundary condition. Alternatively, this can be a (jitable, vectorized) function with signature (adjacent_value, dx, *coords, t) that determines the value of target from the closest field value adjacent_value, the spatial discretization dx in the direction perpendicular to the wall, the spatial coordinates of the wall point, and time t.
target (str) – Selects which value is actually set. Possible choices include value, derivative, and virtual_point.
- class ExpressionValueBC(grid, axis, upper, *, rank=0, value=0, target='value')[source]
Bases:
ExpressionBCrepresents a boundary whose value is calculated from an expression
The expression is given as a string and will be parsed by
sympy. The expression can contain typical mathematical operators and may depend on the value at the last support point next to the boundary (value), spatial coordinates defined by the grid marking the boundary point (e.g., x or r), and time t.Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
value (float or str or callable) – An expression that determines the value of the boundary condition. Alternatively, this can be a (jitable, vectorized) function with signature (adjacent_value, dx, *coords, t) that determines the value of target from the closest field value adjacent_value, the spatial discretization dx in the direction perpendicular to the wall, the spatial coordinates of the wall point, and time t.
target (str) – Selects which value is actually set. Possible choices include value, derivative, and virtual_point.
- class MixedBC(grid, axis, upper, *, rank=0, value=0, const=0)[source]
Bases:
ConstBC1stOrderBaserepresents a mixed (or Robin) boundary condition imposing a derivative in the outward normal direction of the boundary that is given by an affine function involving the actual value:
\[\partial_n c + \gamma c = \beta\]Here, \(c\) is the field to which the condition is applied, \(\gamma\) quantifies the influence of the field and \(\beta\) is the constant term. Note that \(\gamma = 0\) corresponds to Dirichlet conditions imposing \(\beta\) as the derivative. Conversely, \(\gamma \rightarrow \infty\) corresponds to imposing a zero value on \(c\).
This condition can be enforced by using one of the following variants
bc = {'mixed': VALUE} bc = {'type': 'mixed', 'value': VALUE, 'const': CONST}
where VALUE corresponds to \(\gamma\) and CONST to \(\beta\).
- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
value (float or str or array) – The parameter \(\gamma\) quantifying the influence of the field onto its normal derivative. If value is a single value (or tensor in case of tensorial boundary conditions), the same value is applied to all points. Inhomogeneous boundary conditions are possible by supplying an expression as a string, which then may depend on the axes names of the respective grid.
const (float or
ndarrayor str) – The parameter \(\beta\) determining the constant term for the boundary condition. Supports the same input as value.
- copy(upper=None, rank=None, value=None, const=None)[source]
return a copy of itself, but with a reference to the same grid
- get_mathematical_representation(field_name='C')[source]
return mathematical representation of the boundary condition
- get_virtual_point_data(compiled=False)[source]
return data suitable for calculating virtual points
- Parameters:
compiled (bool) – Flag indicating whether a compiled version is required, which automatically takes updated values into account when it is used in numba-compiled code.
- Returns:
the data structure associated with this virtual point
- Return type:
BC1stOrderData
- class NeumannBC(grid, axis, upper, *, rank=0, value=0)[source]
Bases:
ConstBC1stOrderBaserepresents a boundary condition imposing the derivative in the outward normal direction of the boundary
Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur. However, the function is safe when value cannot be an arbitrary string.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
normal (bool) – Flag indicating whether the condition is only applied in the normal direction.
value (float or str or
ndarray) – a value stored with the boundary condition. The interpretation of this value depends on the type of boundary condition. If value is a single value (or tensor in case of tensorial boundary conditions), the same value is applied to all points. Inhomogeneous boundary conditions are possible by supplying an expression as a string, which then may depend on the axes names of the respective grid.
- get_mathematical_representation(field_name='C')[source]
return mathematical representation of the boundary condition
- get_virtual_point_data(compiled=False)[source]
return data suitable for calculating virtual points
- Parameters:
compiled (bool) – Flag indicating whether a compiled version is required, which automatically takes updated values into account when it is used in numba-compiled code.
- Returns:
the data structure associated with this virtual point
- Return type:
BC1stOrderData
- class NormalCurvatureBC(grid, axis, upper, *, rank=0, value=0)[source]
Bases:
CurvatureBCrepresents a boundary condition imposing the 2nd normal derivative onto the normal components at the boundary
Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur. However, the function is safe when value cannot be an arbitrary string.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
normal (bool) – Flag indicating whether the condition is only applied in the normal direction.
value (float or str or
ndarray) – a value stored with the boundary condition. The interpretation of this value depends on the type of boundary condition. If value is a single value (or tensor in case of tensorial boundary conditions), the same value is applied to all points. Inhomogeneous boundary conditions are possible by supplying an expression as a string, which then may depend on the axes names of the respective grid.
- class NormalDirichletBC(grid, axis, upper, *, rank=0, value=0)[source]
Bases:
DirichletBCrepresents a boundary condition imposing the value on normal components
Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur. However, the function is safe when value cannot be an arbitrary string.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
normal (bool) – Flag indicating whether the condition is only applied in the normal direction.
value (float or str or
ndarray) – a value stored with the boundary condition. The interpretation of this value depends on the type of boundary condition. If value is a single value (or tensor in case of tensorial boundary conditions), the same value is applied to all points. Inhomogeneous boundary conditions are possible by supplying an expression as a string, which then may depend on the axes names of the respective grid.
- names: List[str] = ['normal_value', 'normal_dirichlet', 'dirichlet_normal']
identifiers used to specify the given boundary class
- Type:
- class NormalMixedBC(grid, axis, upper, *, rank=0, value=0, const=0)[source]
Bases:
MixedBCrepresents a mixed (or Robin) boundary condition setting the derivative of the normal components in the outward normal direction of the boundary using an affine function involving the actual value:
\[\partial_n c + \gamma c = \beta\]Here, \(c\) is the field to which the condition is applied, \(\gamma\) quantifies the influence of the field and \(\beta\) is the constant term. Note that \(\gamma = 0\) corresponds to Dirichlet conditions imposing \(\beta\) as the derivative. Conversely, \(\gamma \rightarrow \infty\) corresponds to imposing a zero value on \(c\).
This condition can be enforced by using one of the following variants
bc = {'mixed': VALUE} bc = {'type': 'mixed', 'value': VALUE, 'const': CONST}
where VALUE corresponds to \(\gamma\) and CONST to \(\beta\).
- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
value (float or str or array) – The parameter \(\gamma\) quantifying the influence of the field onto its normal derivative. If value is a single value (or tensor in case of tensorial boundary conditions), the same value is applied to all points. Inhomogeneous boundary conditions are possible by supplying an expression as a string, which then may depend on the axes names of the respective grid.
const (float or
ndarrayor str) – The parameter \(\beta\) determining the constant term for the boundary condition. Supports the same input as value.
- names: List[str] = ['normal_mixed', 'normal_robin']
identifiers used to specify the given boundary class
- Type:
- class NormalNeumannBC(grid, axis, upper, *, rank=0, value=0)[source]
Bases:
NeumannBCrepresents a boundary condition imposing the derivative of normal components in the outward normal direction of the boundary
Warning
This implementation uses
exec()and should therefore not be used in a context where malicious input could occur. However, the function is safe when value cannot be an arbitrary string.- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
normal (bool) – Flag indicating whether the condition is only applied in the normal direction.
value (float or str or
ndarray) – a value stored with the boundary condition. The interpretation of this value depends on the type of boundary condition. If value is a single value (or tensor in case of tensorial boundary conditions), the same value is applied to all points. Inhomogeneous boundary conditions are possible by supplying an expression as a string, which then may depend on the axes names of the respective grid.
- names: List[str] = ['normal_derivative', 'normal_neumann', 'neumann_normal']
identifiers used to specify the given boundary class
- Type:
- class UserBC(grid, axis, upper, *, rank=0)[source]
Bases:
BCBaserepresents a boundary whose virtual point are set by the user.
Boundary conditions will only be set when a dictionary
{TARGET: value}is supplied as argument args toset_ghost_cells()or the numba equivalent. Here, TARGET determines how the value is interpreted and what boundary condition is actually enforced: the value of the virtual points directly (virtual_point), the value of the field at the boundary (value) or the outward derivative of the field at the boundary (derivative).Warning
This implies that the boundary conditions are never enforced automatically, e.g., when evaluating an operator. It is thus the user’s responsibility to ensure virtual points are set correctly before operators are applied.
- Parameters:
grid (
GridBase) – The grid for which the boundary conditions are definedaxis (int) – The axis to which this boundary condition is associated
upper (bool) – Flag indicating whether this boundary condition is associated with the upper side of an axis or not. In essence, this determines the direction of the local normal vector of the boundary.
rank (int) – The tensorial rank of the field for this boundary condition
- get_mathematical_representation(field_name='C')[source]
return mathematical representation of the boundary condition
- make_ghost_cell_setter()[source]
return function that sets the ghost cells for this boundary
- Return type:
- make_virtual_point_evaluator()[source]
returns a function evaluating the value at the virtual support point
- Returns:
A function that takes the data array and an index marking the current point, which is assumed to be a virtual point. The result is the data value at this point, which is calculated using the boundary condition.
- Return type:
function
- set_ghost_cells(data_full, *, args=None)[source]
set the ghost cell values for this boundary
- Parameters:
data_full (
ndarray) – The full field data including ghost pointsargs (
ndarray) – Determines what boundary conditions are set. args should be set to{TARGET: value}. Here, TARGET determines how the value is interpreted and what boundary condition is actually enforced: the value of the virtual points directly (virtual_point), the value of the field at the boundary (value) or the outward derivative of the field at the boundary (derivative).
- Return type:
None